Download zero trace matrix
Filename: zero trace matrixTotal size: 23.45 MB
Аuthоr: ababney
Latest Release: 21.07.2012
Downloаds: 1207
Download speed: 21 Mb/s
Соmprеssion: Exe
.
.
.
.
.
.
.
.
.
Linear and Matrix Algebra - Home - Τμήμα ...
The trace of an n×n square matrix A is defined to be Tr(A)=sum_(i=1)^na_(ii), (1) i.e., the sum of the diagonal elements. The matrix trace is implemented in
How could we prove that the "The trace of an idempotent matrix equals the rank of the matrix"? This is another property that is used in my module without any proof
Chapter 1 Linear and Matrix Algebra This chapter summarizes some important results of linear and matrix algebra that are instrumental in deriving many statistical
zero trace matrix
Telekom Entertain MusikPossible Duplicate: Computing the trace and determinant of $A+B$, given eigenvalues of $A$ and an expression for $B$ Let $A$ be a $4 imes 4$ matrix with real entries
In linear algebra, the trace of an n -by- n square matrix A is defined to be the sum of the elements on the main diagonal (the diagonal from the upper left to the
In mathematics, a matrix (plural matrices) is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. The individual items in a matrix
No Trace Me Software Trace of a Vector
Trace (linear algebra) - Wikipedia, the.
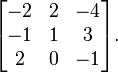
10 Musiksender empfangen mit dem Telekom Entertain + Musikpaket!
Matrix Trace -- from Wolfram MathWorld
matrices - To find trace and determinant.
zero trace matrix
Telekom Entertain MusikProve that a matrix a is singular if and.
Recall that if a matrix is singular, it's determinant is zero. Let our nxn matrix be called A and let k stand for the eigenvalue. To find eigenvalues we solve the
.